
Savin A (1995) In: Chong DP (ed) Recent advances in density functional methods, Part I. Grimme S, Antony J, Ehrlich S, Krieg H (2010) J Chem Phys 132:154104Īustin A, Petersson G, Frisch MJ, Dobek FJ, Scalmani G, Throssell K (2012) J Chem Theory and Comput 8:4989Ĭhai J-D, Head-Gordon M (2008) J Chem Phys 128:084106 Grimme S, Ehrlich S, Goerigk L (2011) J Comput Chem 32:1456 Peverati R, Truhlar DG (2011) J Phys Chem Lett 2:2810 Stephens PJ, Devlin FJ, Chabalowski CF, Frisch MJ (1994) J Phys Chem 98:11623 Yanai T, Tew DP, Handy NC (2004) Chem Phys Lett 393:51 Tawada T, Tsuneda T, Yanagisawa S, Yanai T, Hirao K (2004) J Chem Phys 120:8425 Sato T, Tsuneda T, Hirao K (2005) Mol Phys 103:1151 Kamiya M, Tsuneda T, Hirao K (2002) J Chem Phys 117:6010 Iikura H, Tsuneda T, Yanai T, Hirao K (2001) J Chem Phys 115:3540 Goll E, Werner HJ, Stoll H, Leininger T, Gori-Giorgi P, Savin A (2006) Chem Phys 329:276 Mourik TV, Gdanitz RJ (2002) J Chem Phys 116:9620Īndersson Y, Langreth DC, Lundqvist BI (1996) Phys Rev Lett 76:102 Kohn W, Meir Y, Makarov DE (1998) Phys Rev Lett 80:4153 Leininger T, Stoll H, Werner H-J, Savin A (1887) Chem Phys Lett 275:151 Hohenberg P, Kohn W (1964) Phys Rev B 136:864 Successes are obtained also for the Grimme B97D functional, when coupled with the D2 and D3 dispersion scheme, the results being rather independent from the basis set, as expected from the empirical nature of this type of amendment. While the vast majority of the tested functionals undergo failures, good results are obtained for some long-range-corrected functionals (LC-BLYP and LC-wPBE), which follow the Tsuneda and Hirao’s scheme, provided that richer basis sets (with diffuse components) are used.
GNU OCTAVE PCE FUNCTION SERIES
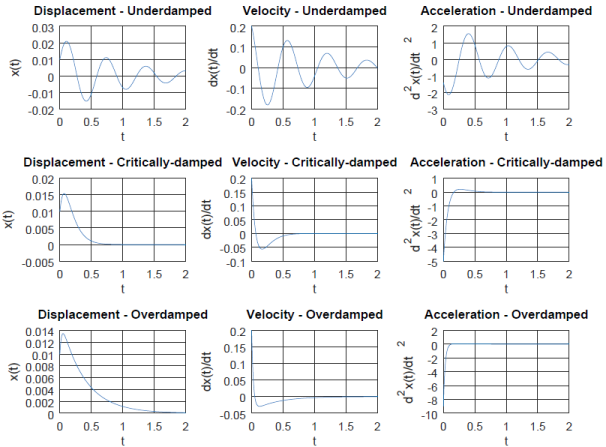
A phenomenological model, based on transparent analytical formulas of the totally symmetric modes, is outlined and used to assess the computational results on series of functionals belonging to different classes (genuine forms, long-range corrected and with empiric dispersion ingredients). The energy scale of the investigated vibrations is comparable to that of the extracted van der Waals interaction parameters, achieving then a well-tempered description. We designed a procedure based on the shifts of vibrational frequencies in C 60 versus 60 couples. The particular case of endohedral noble gas atoms in C 60 fullerene puts several methodological challenges, such as the numeric problem in the balance of covalent versus non-covalent interactions. Also, I am yet to encounter a single case where arrayfun/pararrayfun beats simple vectorization (or simple vectorization combined with parfor).This work is dedicated to a special test, checking the capability of density functional theory computations in the account of long-range effects. While I cannot answer your question (as I cannot reproduce the error), I would suggest you not to use pararrayfun for this case. % Simple vectorization to let Octave figure out the threading itself. % Uses half the amount of time and 1/64th of the cores. % pararrayfun using 1 thread with ChunksPerProc = 1. % (in theory) decreases time on busy machines, but in my case it didn't help. I am on a machine with 64 threads and here are the timing results % pararrayfun using all available threads with ChunksPerProc = 1. However, apparently the Octave interpreter is not smart enough. In my experience, MATLAB's JIT compiler is smart enough to vectorize simple for loops like we have here. I have a philosophical issue with arrayfun / pararrayfun ( What is the use of arrayfun if a for loop is faster?), I believe that they are completely redundant, and they fool MATLAB/Octave users into false sense of efficiency.
I was fooling around and testing some other options to do the same calculation and comparing the time spent for each one. Vector_y = pararrayfun(1, 10.*log10(x.^2), vector_x, "Vectorized", true, "ChunksPerProc", 1) Vector_y = pararrayfun(nproc, 10.*log10(x.^2), vector_x, "Vectorized", true, "ChunksPerProc", 1) Here is the snippet I am using: pkg load parallel


 0 kommentar(er)
0 kommentar(er)
